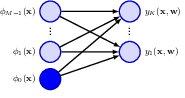
4 Single layer networks: regression
In machine learning we often use x to denote the input data and y to denote the target. If we only have x but not y, this is a unsupervised learning problem, which means that we have some data, but we don’t specifically have a task to take advantage of them. In this case we can use the probability theory we have just introduced to model their distributions. If we have both x and y, we’d often want to know how having x giving rise to the realization of y, and this will be a supervised learning problem. In this case not only do we want to model the distribution of y, we also want to know how the distribution of y can be affected by the value of x.
Depending on the nature of y supervised learning problems can be further categorized into regression and classification. Regression when y is continuous and classification when it’s discrete. We can talk about regression and classification all day long: they are the backbone of many statistical models used in many natural science and social science fields. But here we are only using them as components of deep neural networks, which we plan to build in later chapters.
4.1 Linear regression
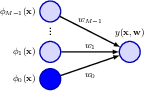
4.1.1 Basis function
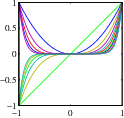
Extending simple linear regression with basis functions.
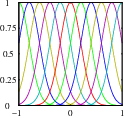
Some basis functions are more localised than others.
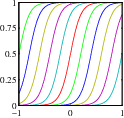
4.1.2 Likelihood function
\[ \begin{align} \ln p(\mathbf{t} | \mathbf{X}, \mathbf{w}, \sigma^2) &= \sum_{n=1}^{N} \ln \mathcal{N}(t_n | \mathbf{w}^\top \mathbf{\phi}(\mathbf{x}_n), \sigma^2) \\ &= \sum_{n=1}^{N} \ln \left( \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left\{ -\frac{1}{2\sigma^2} (t_n - \mathbf{w}^\top \mathbf{\phi}(\mathbf{x}_n))^2 \right\} \right) \\ &= -\frac{N}{2} \ln (2\pi\sigma^2) - \frac{1}{2\sigma^2} E_D(\mathbf{w}) \end{align} \]
where the sum-of-squares error function is defined by
\[ E_D(\mathbf{w}) = \frac{1}{2} \sum_{n=1}^{N} \left\{ t_n - \mathbf{w}^\top \mathbf{\phi}(\mathbf{x}_n) \right\}^2. \]
4.1.3 Maximum likelihood
4.1.4 Geometry of least squares
Geometrically, the least squares solution is the orthogonal projection of the target onto the subspace spanned by the basis functions.
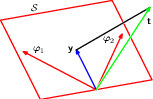
4.1.5 Sequential learning
4.1.6 Regularised least squares
4.1.7 Multiple outputs